miércoles, 28 de enero de 2015
lunes, 19 de enero de 2015
¿Grafo Perfecto?
Es un grafo en el que el numero cromatico de cada subgrafo inducido es igual al tamaño del mayor clique de ese subgrafo.
En cualquier grafo, el número clique provee una cota inferior para el número cromático, ya que a cada uno de los vértices en un clique se les debe asignar un color distinto para obtener una coloración propia. Los grafos perfectos son aquellos para los cuales esta cota inferior es exacta no sólo para el grafo en sí, sino para todos los subgrafos inducidos. En los grafos en general, el número cromático y el número de clique pueden ser distintos. Por ejemplo, un ciclo de 5 vértices requiere tres colores para obtener una coloración correcta, pero el clique mayor es de tamaño dos.
En cualquier grafo, el número clique provee una cota inferior para el número cromático, ya que a cada uno de los vértices en un clique se les debe asignar un color distinto para obtener una coloración propia. Los grafos perfectos son aquellos para los cuales esta cota inferior es exacta no sólo para el grafo en sí, sino para todos los subgrafos inducidos. En los grafos en general, el número cromático y el número de clique pueden ser distintos. Por ejemplo, un ciclo de 5 vértices requiere tres colores para obtener una coloración correcta, pero el clique mayor es de tamaño dos.
¿Grafo Rueda?
es un grafo con n vertices que se forma conectando un único vértice a todos los vértices de un cliclo(n-1).
Los grafos rueda son grafos planos,
y como tales pueden ser "incrustado" en un plano. Más específicamente,
todo gráfico rueda es un grafo de Halin. Son auto-duales: el dual de cualquier grafo rueda es un grafo.
¿Grafo plano?
Es un grafo que puede ser dibujado en el plano sin que ninguna aristase cruce (una definición más formal puede ser que este grafo pueda ser "incrustado" en un plano). Los grafos K5 y el K3,3 son los grafos no planos minimales, lo cual nos permitirán caracterizar el resto de los grafos no planos.
Todo grafo plano puede ser dibujado sobre la esfera, y viceversa. Una generalización de los grafos planos son grafos dibujados e incrustados sobre superficies de generoarbitrario. En esta terminología, los grafos planos tienen genero 0, por ser el plano y la esfera de género 0.
Todo grafo plano puede ser dibujado sobre la esfera, y viceversa. Una generalización de los grafos planos son grafos dibujados e incrustados sobre superficies de generoarbitrario. En esta terminología, los grafos planos tienen genero 0, por ser el plano y la esfera de género 0.
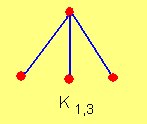
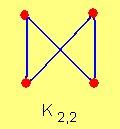
¿Grafo Bipartito Completo?
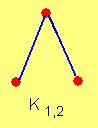
Es un grafo bipartito tal que 
Es decir, un grafo bipartito completo está formado por dos conjuntos disjuntos de vértices y todas las posibles aristas que unen esos vértices.
El grafo completo bipartito con particiones de tamaño
y 
es denotado como 
.
Es decir, un grafo bipartito completo está formado por dos conjuntos disjuntos de vértices y todas las posibles aristas que unen esos vértices.El grafo completo bipartito con particiones de tamaño
y es denotado como .
¿Grafo BiPartito ?
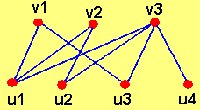
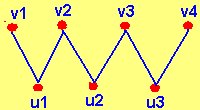
Se denomina al grafo cuyos vértices se pueden separar en dos subconjuntos disjuntos V1(G) y V2(G) y las líneas siempre unen vértices de un subconjunto con vértices de otro subconjunto. Además se tiene que:
Un grafo bipartido en el cual todos los elementos de V1 están unidos con todos los elementos de V2 se denomina grafo bipartido completo.
- V1(G) U V2(G) = V(G).
- La intersección de V1(G) y V2(G) es vacío.
- Para todos los puntos x1, x2 en V1(G) y para todos los puntos y1, y2 en V2(G) , no existe línea alguna x = (x1,x2) , ni x = (y1,y2).
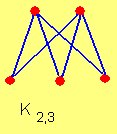
A continuación, mostramos dos ejemplos de grafos bipartidos donde /V1(G)/ = 3 y /V2(G)/= 4
.
Un grafo bipartido en el cual todos los elementos de V1 están unidos con todos los elementos de V2 se denomina grafo bipartido completo.
El
conjunto de los grafos bipartidos completos es denominado con la letra
K. En particular, un grafo completo bipartido que une dos conjuntos, de m
y n elementos respectivamente, se denota por Km,n. Es obvio que Km,n tiene p=(m+n) vértices y q=mn líneas.
¿Grafo Simple?
Es aquel que acepta
una sola arista uniendo dos vértices cualesquiera. Esto es equivalente a
decir que una arista cualquiera es la única que une dos vértices
específicos. Es la definición estándar de un grafo.
¿Adyacencia, Insidencia,Ponderacón,Etiquetado?
- Adyacencia: dos aristas son adyacentes si tienen un vértice en común, y dos vértices son adyacentes si una arista los une.
- Incidencia: una arista es incidente a un vértice si ésta lo une a otro.
- Ponderación: corresponde a una función que a cada arista le asocia un valor (costo, peso, longitud, etc.), para aumentar la expresividad del modelo. Esto se usa mucho para problemas de optimización, como el del vendedor del viajero o del camino mas corto.
- Etiquetado: distinción que se hace a los vértices y/o aristas mediante una marca que los hace unívocamente distinguibles del resto.
¿MultiGrafos o Pseudografos?
- V es un conjunto de vértices o nodos
- E es un multiconjunto de pares no ordenados de nodos, llamados aristas o líneas
¿Grafos Mixtos?
Un grafo mixto es aquel que se define con la capacidad de poder
contener aristas dirigidas y no dirigidas. Tanto los grafos dirigidos
como los no dirigidos son casos particulares de este.
¿Grafo no dirigido?
Un grafo en el cual todas las aristas son no dirigidas se denominará
"grafo no dirigido". El grafo no dirigido es aquel que no tiene sentido
su arista. Un grafo no dirigido G representa elementos, y una arista (v,
w) representa una incompatibilidad entre los elementos v y w.
¿Grafos Dirigidos?
¿Que son Grafos?
Representación simbólica de los elementos constituidos de un sistema o conjunto, mediante esquemas gráficos.
Suscribirse a:
Entradas (Atom)