¿Grafo BiPartito ?

Se denomina al grafo cuyos vértices se pueden separar en dos subconjuntos disjuntos V1(G) y V2(G) y las líneas siempre unen vértices de un subconjunto con vértices de otro subconjunto. Además se tiene que:

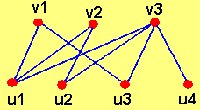
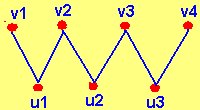
• V1(G) U V2(G) = V(G).
• La intersección de V1(G) y V2(G) es vacío.
• Para todos los puntos x1, x2 en V1(G) y para todos los puntos y1, y2 en V2(G) , no existe línea alguna x = (x1,x2) , ni x = (y1,y2).

A continuación, mostramos dos ejemplos de grafos bipartidos donde /V1(G)/ = 3 y /V2(G)/= 4

.

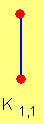
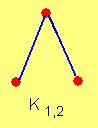
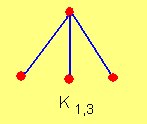
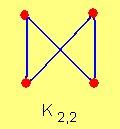
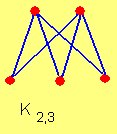
Un grafo bipartido en el cual todos los elementos de V1 están unidos con todos los elementos de V2 se denomina grafo bipartido completo.

El conjunto de los grafos bipartidos completos es denominado con la letra K. En particular, un grafo completo bipartido que une dos conjuntos, de m y n elementos respectivamente, se denota por Km,n. Es obvio que Km,n tiene p=(m+n) vértices y q=mn líneas.